こんにちは、高3担当の坂井です。

金沢大学の数物科学類に所属しており、主に数学を勉強しています。

皆さんは数学が好きでしょうか？

なるほどなるほど、僕は好きです！

もちろん計算が煩雑で逃げ出すことや

理解できないと投げ出したことなど数え切れないほどありますが…　

そんな僕が今回皆さんに紹介したいものは「鳩の巣原理」です。

/

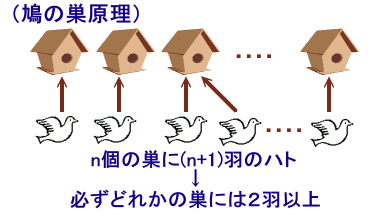
鳩の巣原理とはｎ羽の鳩とｍ個の巣がある。

このときｎ＞mならば少なくとも１つの巣には2羽以上いるというものです。

10羽の鳩に対して巣が8個しかなければ2羽以上の鳩がいる巣が存在する。

こんなの当たり前じゃないかと思う人も多いでしょうが

これも立派な原理のひとつです。

/

/

/

問　ランダムで相異なる5つの整数a,b,c,d,eを選ぶ。

このとき、その差が4の倍数となる整数の組が少なくとも１つは存在することを示せ。

/

これが鳩の巣原理を使う問題の典型例です。

詳しい解説は省きますが、4のあまりが0,1,2,3、のいずれかのため、

鳩の巣原理より5つ整数を選ぶと必ずあまりが同じとなる組が存在します。

その組の差をとってあげると

あまりの部分が打ち消しあうので必ず４の倍数になるという証明の流れです。

/

正直僕は初めて鳩の巣原理を知った時、

「こんなの当たり前のことを言ってるだけじゃん」となめていました。

しかしいざ問題を解いてみると、

どれを鳩とみなしてどれを巣とみなすかを考えることで、

こんなすごい問題を解くことができるのかと感動し、

この原理が好きになりました。（原理の説明に鳩や巣を使っているのも素敵ですね）

/

この原理はドイツの数学者ペーター・グスタフ・ディリクレさんが提唱しました。

鳩の巣原理のほかにも彼の名前の付いた原理や定理は多く存在するので

興味のある方は調べてみてください。

/

　これからも数学について何かしらつづっていけたらと思っているので、

こんな数学もあるんだと楽しんでもらえたら幸いです。

もしこのブログを読んで深く数学を学びたいと思ってくれた方、ぜひぜひ数学科へ!!